Portal:Mathematics

---

The Mathematics Portal

Carl Friedrich Gauss

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Featured articles –

  Featured articles are displayed here, which represent some of the best content on English Wikipedia.

---

• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
• 
  General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
  present, including matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.
  
  Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
• 
  
  

  

  One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

  
  Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.
  
  Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
• 
  
  

  

  Portrait by August Köhler, c. 1910, after 1627 original

  
  Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ^ⓘ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.
  
  Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
  Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
• 
  
  

  

  Rejewski, c. 1932

  
  Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ^ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
  
  Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
• 
  In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.
  
  Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
• 

  

  High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

  
  
  General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.
  
  By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
• 

  

  Plots of logarithm functions, with three commonly used bases. The special points log_b b = 1 are indicated by dotted lines, and all curves intersect in log_b 1 = 0.

  
  
  In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the 3rd power: 1000 = 10³ = 10 × 10 × 10. More generally, if x = b^y, then y is the logarithm of x to base b, written log_b x, so log₁₀ 1000 = 3. As a single-variable function, the logarithm to base b is the inverse of exponentiation with base b.
  
  The logarithm base 10 is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number e ≈ 2.718 as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base 2 and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written log x. (Full article...)
• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's first and second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 
  The number π (/paɪ/ ^ⓘ; spelled out as pi) is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.
  
  The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as ${\tfrac {22}{7}}$ are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
• 
  
  

  

  Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

  
  An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.
  
  While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in 17th-century studies of probability and annuities. Actuaries in the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems; actuaries use this knowledge to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
• 
  
  

  

  Kaczynski after his arrest in 1996

  
  Theodore John Kaczynski (/kəˈzɪnski/ ^ⓘ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ ^ⓘ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle and lone wolf terrorism campaign to further his political agenda.
  
  Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored a roughly 35,000-word manifesto and social critique called Industrial Society and Its Future which opposes all forms of technology, rejects leftism and fascism, advocates primitivism, and ultimately suggests violent revolution. (Full article...)
• 
  
  

  

  Elementary algebra studies which values solve equations formed using arithmetical operations.

  
  Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
  
  Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
• 

  

  The manipulations of the Rubik's Cube form the Rubik's Cube group.

  
  In mathematics, a group is a set with a binary operation that satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.
  
  Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠$1$⁠ (these properties characterize the integers in a unique way). (Full article...)
• 

  

  Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

  
  
  In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
  
  In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)

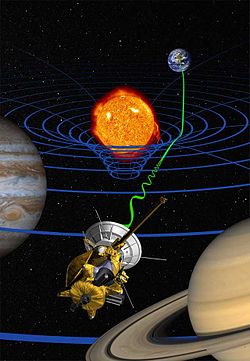
Selected image –

diagram of a unit circle and several associated triangles whose side lengths are the values of the various trigonometric functions

Trigonometric function

Credit: Steven G. Johnson (original version)

This is a graphical construction of the various trigonometric functions from a unit circle centered at the origin, O, and two points, A and D, on the circle separated by a central angle θ. The triangle AOC has side lengths cos θ (OC, the side adjacent to the angle θ) and sin θ (AC, the side opposite the angle), and a hypotenuse of length 1 (because the circle has unit radius). When the tangent line AE to the circle at point A is drawn to meet the extension of OD beyond the limits of the circle, the triangle formed, AOE, contains sides of length tan θ (AE) and sec θ (OE). When the tangent line is extended in the other direction to meet the line OF drawn perpendicular to OC, the triangle formed, AOF, has sides of length cot θ (AF) and csc θ (OF). In addition to these common trigonometric functions, the diagram also includes some functions that have fallen into disuse: the chord (AD), versine (CD), exsecant (DE), coversine (GH), and excosecant (FH). First used in the early Middle Ages by Indian and Islamic mathematicians to solve simple geometrical problems (e.g., solving triangles), the trigonometric functions today are used in sophisticated two- and three-dimensional computer modeling (especially when rotating modeled objects), as well as in the study of sound and other mechanical waves, light (electromagnetic waves), and electrical networks.

Good articles –

  These are Good articles, which meet a core set of high editorial standards.

---

• 
  Fermat's Last Tango is a 2000 off-Broadway musical about the proof of Fermat's Last Theorem, written by husband and wife Joshua Rosenblum (music, lyrics) and Joanne Sydney Lessner (book, lyrics). The musical presents a fictionalized version of the real life story of Andrew Wiles, and has been praised for the accuracy of the mathematical content. The original production at the York Theatre received mixed reviews, but the musical was well received by mathematical audiences. A video of the original production has been distributed by the Clay Mathematics Institute and shown at several mathematical conferences and similar occasions. The musical has also been translated into Portuguese. (Full article...)
• 
  
  

  

  Hugo Steinhaus (1968)

  
  Hugo Dyonizy Steinhaus (English: /ˈhjuːɡoʊ ˈstaɪnhaʊs/ HEW-goh STYNE-howss; Polish: [ˈxuɡɔ ˈʂtajnxaws]; German: [ˈhuːɡoː ˈʃtaɪnhaʊs]; 14 January 1887 – 25 February 1972) was a Polish mathematician and educator. Steinhaus obtained his PhD under David Hilbert at Göttingen University in 1911 and later became a professor at the Jan Kazimierz University in Lwów (now Lviv, Ukraine), where he helped establish what later became known as the Lwów School of Mathematics. He is credited with "discovering" mathematician Stefan Banach, with whom he gave a notable contribution to functional analysis through the Banach–Steinhaus theorem. After World War II Steinhaus played an important part in the establishment of the mathematics department at Wrocław University and in the revival of Polish mathematics from the destruction of the war.
  
  Author of around 170 scientific articles and books, Steinhaus has left his legacy and contribution in many branches of mathematics, such as functional analysis, geometry, mathematical logic, and trigonometry. Notably he is regarded as one of the early founders of game theory and probability theory, which led to later development of more comprehensive approaches by other scholars. (Full article...)
• 
  
  

  

  An ideal regular octahedron in the Poincaré ball model of hyperbolic space (sphere at infinity not shown). All dihedral angles of this shape are right angles.

  
  In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.
  
  The Platonic solids and Archimedean solids have ideal versions, with the same combinatorial structure as their more familiar Euclidean versions. Several uniform hyperbolic honeycombs divide hyperbolic space into cells of these shapes, much like the familiar division of Euclidean space into cubes. However, not all polyhedra can be represented as ideal polyhedra – a polyhedron can be ideal only when it can be represented in Euclidean geometry with all its vertices on a circumscribed sphere. Using linear programming, it is possible to test whether a polyhedron has an ideal version, in polynomial time. (Full article...)
• 

  

  Four opaque sets for a unit square. Upper left: its boundary, length 4. Upper right: Three sides, length 3. Lower left: a Steiner tree of the vertices, length $1+{\sqrt {3}}\approx 2.732$. Lower right: the conjectured optimal solution, length ${\sqrt {2}}+{\tfrac {1}{2}}{\sqrt {6}}\approx 2.639$.

  
  In discrete geometry, an opaque set is a system of curves or other set in the plane that blocks all lines of sight across a polygon, circle, or other shape. Opaque sets have also been called barriers, beam detectors, opaque covers, or (in cases where they have the form of a forest of line segments or other curves) opaque forests. Opaque sets were introduced by Stefan Mazurkiewicz in 1916, and the problem of minimizing their total length was posed by Frederick Bagemihl in 1959.
  
  For instance, visibility through a unit square can be blocked by its four boundary edges, with length 4, but a shorter opaque forest blocks visibility across the square with length ${\sqrt {2}}+{\tfrac {1}{2}}{\sqrt {6}}\approx 2.639$. It is unproven whether this is the shortest possible opaque set for the square, and for most other shapes this problem similarly remains unsolved. The shortest opaque set for any bounded convex set in the plane has length at most the perimeter of the set, and at least half the perimeter. For the square, a slightly stronger lower bound than half the perimeter is known. Another convex set whose opaque sets are commonly studied is the unit circle, for which the shortest connected opaque set has length $2+\pi$. Without the assumption of connectivity, the shortest opaque set for the circle has length at least $\pi$ and at most $4.7998$. (Full article...)
• 
  1 (one, unit, unity) is a number, numeral, and glyph. It is the first and smallest positive integer of the infinite sequence of natural numbers. This fundamental property has led to its unique uses in other fields, ranging from science to sports, where it commonly denotes the first, leading, or top thing in a group. 1 is the unit of counting or measurement, a determiner for singular nouns, and a gender-neutral pronoun. Historically, the representation of 1 evolved from ancient Sumerian and Babylonian symbols to the modern Arabic numeral.
  
  In mathematics, 1 is the multiplicative identity, meaning that any number multiplied by 1 equals the same number. 1 is by convention not considered a prime number. In digital technology, 1 represents the "on" state in binary code, the foundation of computing. Philosophically, 1 symbolizes the ultimate reality or source of existence in various traditions. (Full article...)
• 

  

  A Halin graph

  
  In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle.
  The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross (this is called a planar embedding), and the cycle
  connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.
  
  Halin graphs are named after German mathematician Rudolf Halin, who studied them in 1971.
  The cubic Halin graphs – the ones in which each vertex touches exactly three edges – had already been studied over a century earlier by Kirkman.
  Halin graphs are polyhedral graphs, meaning that every Halin graph can be used to form the vertices and edges of a convex polyhedron, and the polyhedra formed from them have been called roofless polyhedra or domes. (Full article...)
• 

  

  Euclidean minimum spanning tree of 25 random points in the plane

  
  
  A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.
  
  The edges of the minimum spanning tree meet at angles of at least 60°, at most six to a vertex. In higher dimensions, the number of edges per vertex is bounded by the kissing number of tangent unit spheres. The total length of the edges, for points in a unit square, is at most proportional to the square root of the number of points. Each edge lies in an empty region of the plane, and these regions can be used to prove that the Euclidean minimum spanning tree is a subgraph of other geometric graphs including the relative neighborhood graph and Delaunay triangulation. By constructing the Delaunay triangulation and then applying a graph minimum spanning tree algorithm, the minimum spanning tree of $n$ given planar points may be found in time $O(n\log n)$, as expressed in big O notation. This is optimal in some models of computation, although faster randomized algorithms exist for points with integer coordinates. For points in higher dimensions, finding an optimal algorithm remains an open problem. (Full article...)
• 
  The Euclid–Euler theorem is a theorem in number theory that relates perfect numbers to Mersenne primes. It states that an even number is perfect if and only if it has the form 2^p−1(2^p − 1), where 2^p − 1 is a prime number. The theorem is named after mathematicians Euclid and Leonhard Euler, who respectively proved the "if" and "only if" aspects of the theorem.
  
  It has been conjectured that there are infinitely many Mersenne primes. Although the truth of this conjecture remains unknown, it is equivalent, by the Euclid–Euler theorem, to the conjecture that there are infinitely many even perfect numbers. However, it is also unknown whether there exists even a single odd perfect number. (Full article...)
• 

  

  The brute force algorithm finds a 4-clique in this 7-vertex graph (the complement of the 7-vertex path graph) by systematically checking all C(7,4) = 35 4-vertex subgraphs for completeness.

  
  
  In computer science, the clique problem is the computational problem of finding cliques (subsets of vertices, all adjacent to each other, also called complete subgraphs) in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique (a clique with the largest possible number of vertices), finding a maximum weight clique in a weighted graph, listing all maximal cliques (cliques that cannot be enlarged), and solving the decision problem of testing whether a graph contains a clique larger than a given size.
  
  The clique problem arises in the following real-world setting. Consider a social network, where the graph's vertices represent people, and the graph's edges represent mutual acquaintance. Then a clique represents a subset of people who all know each other, and algorithms for finding cliques can be used to discover these groups of mutual friends. Along with its applications in social networks, the clique problem also has many applications in bioinformatics, and computational chemistry. (Full article...)
• 
  
  

  

  Equilateral form of the Cairo tiling

  
  In geometry, a Cairo pentagonal tiling is a tessellation of the Euclidean plane by congruent convex pentagons, formed by overlaying two tessellations of the plane by hexagons and named for its use as a paving design in Cairo. It is also called MacMahon's net after Percy Alexander MacMahon, who depicted it in his 1921 publication New Mathematical Pastimes. John Horton Conway called it a 4-fold pentille.
  
  Infinitely many different pentagons can form this pattern, belonging to two of the 15 families of convex pentagons that can tile the plane. Their tilings have varying symmetries; all are face-symmetric. One particular form of the tiling, dual to the snub square tiling, has tiles with the minimum possible perimeter among all pentagonal tilings. Another, overlaying two flattened tilings by regular hexagons, is the form used in Cairo and has the property that every edge is collinear with infinitely many other edges. (Full article...)
• 
  
  

  

  A Pythagorean tiling

  
  A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern,
  but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.
  
  This tiling has four-way rotational symmetry around each of its squares. When the ratio of the side lengths of the two squares is an irrational number such as the golden ratio, its cross-sections form aperiodic sequences with a similar recursive structure to the Fibonacci word. Generalizations of this tiling to three dimensions have also been studied. (Full article...)
• 

  

  A unit distance graph with 16 vertices and 40 edges

  
  In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.
  
  An unsolved problem of Paul Erdős asks how many edges a unit distance graph on $n$ vertices can have. The best known lower bound is slightly above linear in $n$—far from the upper bound, proportional to $n^{4/3}$. The number of colors required to color unit distance graphs is also unknown (the Hadwiger–Nelson problem): some unit distance graphs require five colors, and every unit distance graph can be colored with seven colors. For every algebraic number there is a unit distance graph with two vertices that must be that distance apart. According to the Beckman–Quarles theorem, the only plane transformations that preserve all unit distance graphs are the isometries. (Full article...)

Did you know (auto-generated) –

• ... that ten-sided gaming dice have kite-shaped faces?
• ... that more than 60 scientific papers authored by mathematician Paul Erdős were published posthumously?
• ... that Ewa Ligocka cooked another mathematician's goose?
• ... that despite published scholarship to the contrary, Andrew Planta neither received a doctorate nor taught mathematics at Erlangen?
• ... that the music of math rock band Jyocho has been alternatively described as akin to "madness" or "contemplative and melancholy"?
• ... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?
• ... that two members of the French parliament were killed when a delayed-action German bomb exploded in the town hall at Bapaume on 25 March 1917?
• ... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?

More did you know –

Did you know...

• ...that the Electronic Frontier Foundation funds awards for the discovery of prime numbers beyond certain sizes?
• ...that pi can be computed using only the number 2 by the work of Viète?
• … that the Riemann Hypothesis, one of the Millennium Problems, depends on the asymptotic growth of the Mertens Function?
• … that every positive integer can be written as the sum of three palindromic numbers in every number system with base 5 or greater?
• … that the best known lower bound for the length of the smallest superpermutation was first posted anonymously to the internet imageboard 4chan?
• ...that the mathematician Grigori Perelman was offered a Fields Medal in 2006, in part for his proof of the Poincaré conjecture, which he declined?
• ...that a regular heptagon is the regular polygon with the fewest sides which is not constructible with a compass and straightedge?

Selected article –

The real part (red) and imaginary part (blue) of the critical line Re(s) = 1/2 of the Riemann zeta-function. Image credit: User:Army1987

The Riemann hypothesis, first formulated by Bernhard Riemann in 1859, is one of the most famous unsolved problems. It has been an open question for well over a century, despite attracting concentrated efforts from many outstanding mathematicians.

The Riemann hypothesis is a conjecture about the distribution of the zeros of the Riemann zeta-function ζ(s). The Riemann zeta-function is defined for all complex numbers s ≠ 1. It has zeros at the negative even integers (i.e. at s=-2, s=-4, s=-6, ...). These are called the trivial zeros. The Riemann hypothesis is concerned with the non-trivial zeros, and states that:

The real part of any non-trivial zero of the Riemann zeta function is ½

Thus the non-trivial zeros should lie on the so-called critical line ½ + it with t a real number and i the imaginary unit. The Riemann zeta-function along the critical line is sometimes studied in terms of the Z-function, whose real zeros correspond to the zeros of the zeta-function on the critical line.

The Riemann hypothesis is one of the most important open problems in contemporary mathematics; a $1,000,000 prize has been offered by the Clay Mathematics Institute for a proof. Most mathematicians believe the Riemann hypothesis to be true. (J. E. Littlewood and Atle Selberg have been reported as skeptical. Selberg's skepticism, if any, waned, from his young days. In a 1989 paper, he suggested that an analogue should hold for a much wider class of functions, the Selberg class.) (Full article...)

View all selected articles

Subcategories

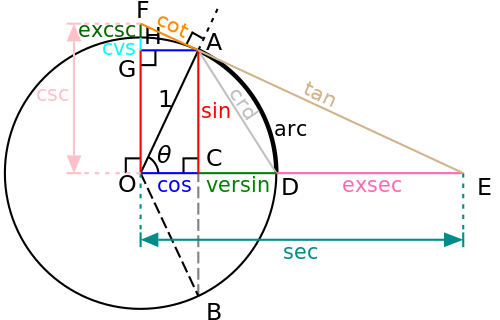
Algebra | Arithmetic | Analysis | Complex analysis | Applied mathematics | Calculus | Category theory | Chaos theory | Combinatorics | Dynamical systems | Fractals | Game theory | Geometry | Algebraic geometry | Graph theory | Group theory | Linear algebra | Mathematical logic | Model theory | Multi-dimensional geometry | Number theory | Numerical analysis | Optimization | Order theory | Probability and statistics | Set theory | Statistics | Topology | Algebraic topology | Trigonometry | Linear programming

---

Mathematics | History of mathematics | Mathematicians | Awards | Education | Literature | Notation | Organizations | Theorems | Proofs | Unsolved problems

Full category tree. Select [►] to view subcategories.

Mathematics

Mathematics by country

Fields of mathematics

Mathematics-related lists

Mathematicians

Women in mathematics

Works about mathematics

Mathematics and art

Bruhat family

Choquet family

Mathematical classification systems

Mathematical concepts

Mathematical constants

Mathematics and culture

Eponyms in mathematics

Mathematical examples

FL-Class Polyhedra articles

History of mathematics

Mathematics occupations

Mathematical notation

Outlines of mathematics and logic

Philosophy of mathematics

Mathematical projects

Mathematical proofs

Pseudomathematics

Set index articles on mathematics

Mathematical terminology

Mathematical theorems

Mathematical tools

Mathematics stubs

Topics in mathematics

General	Foundations	Number theory	Discrete mathematics
Mathematicians History of mathematics Philosophy of mathematics Mathematical notation Mathematical beauty Mathematics education Glossary of mathematical symbols	Foundations of mathematics Mathematical logic Proof theory Gödel's incompleteness theorems Model theory Recursion theory Set theory Naive set theory Axiomatic set theory Category theory Topos theory	Number theory Algebraic number theory Analytic number theory Arithmetic Fundamental theorem of arithmetic Numbers Natural numbers Prime numbers Rational numbers Algebraic numbers	Discrete mathematics Combinatorics Combinatorial geometry Coding theory Combinatorial design Enumerative combinatorics Combinatorial optimization Graph theory Order theory Lattice theory Digital Signal Processing Theoretical computer science Computability theory Complexity theory
Algebra	Analysis	Geometry and topology	Applied mathematics
Algebra Elementary algebra Abstract algebra Group theory Ring theory Field theory Commutative algebra Geometric algebra Linear algebra Matrix theory Multilinear algebra Universal algebra Fundamental theorem of algebra	Analysis Calculus Fundamental theorem of calculus Vector calculus Geometric calculus Measure theory Real analysis Complex analysis Differential equations Ordinary differential equations Partial differential equations Integral equations Approximation theory Special functions Potential theory Harmonic analysis Fourier analysis Functional analysis Operator theory	Geometry Euclidean geometry Trigonometry Analytic geometry Non-Euclidean geometry Affine geometry Projective geometry Convex geometry Discrete geometry Algebraic geometry Differential geometry K theory Gauge theory Riemannian geometry Lie groups Topology General topology Algebraic topology Geometric topology Differential topology	Applied mathematics Mathematical modeling Mathematical physics Dynamical systems Control theory Calculus of variations Optimization Mathematical economics Game theory Mathematical finance Statistics Probability theory Stochastic processes Numerical analysis Cryptography Information theory

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Related portals

WikiProjects

The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.

Project pages

• Participants
• Current activity
• Manual of style
• Conventions

Essays

• Advice on using Wikipedia for mathematics self-study
• Proofs

Subprojects

• PlanetMath Exchange (Talk)
• Graphics (Talk)
• Article assessment (Talk)

Related projects

Computer science | Cryptography | Game theory | Numbers | Physics | Science | Statistics

Things you can do

• Create a new article: List of requested articles
• Add a new image: Image requests
• Expand an article: Mathematics stubs
• Lend your expertise: Expert attention needed

In other Wikimedia projects

The following Wikimedia Foundation sister projects provide more on this subject:

• 

  Commons
  Free media repository

• 

  Wikibooks
  Free textbooks and manuals

• 

  Wikidata
  Free knowledge base

• 

  Wikinews
  Free-content news

• 

  Wikiquote
  Collection of quotations

• 

  Wikisource
  Free-content library

• 

  Wikiversity
  Free learning tools

• 

  Wiktionary
  Dictionary and thesaurus

More portals

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals